
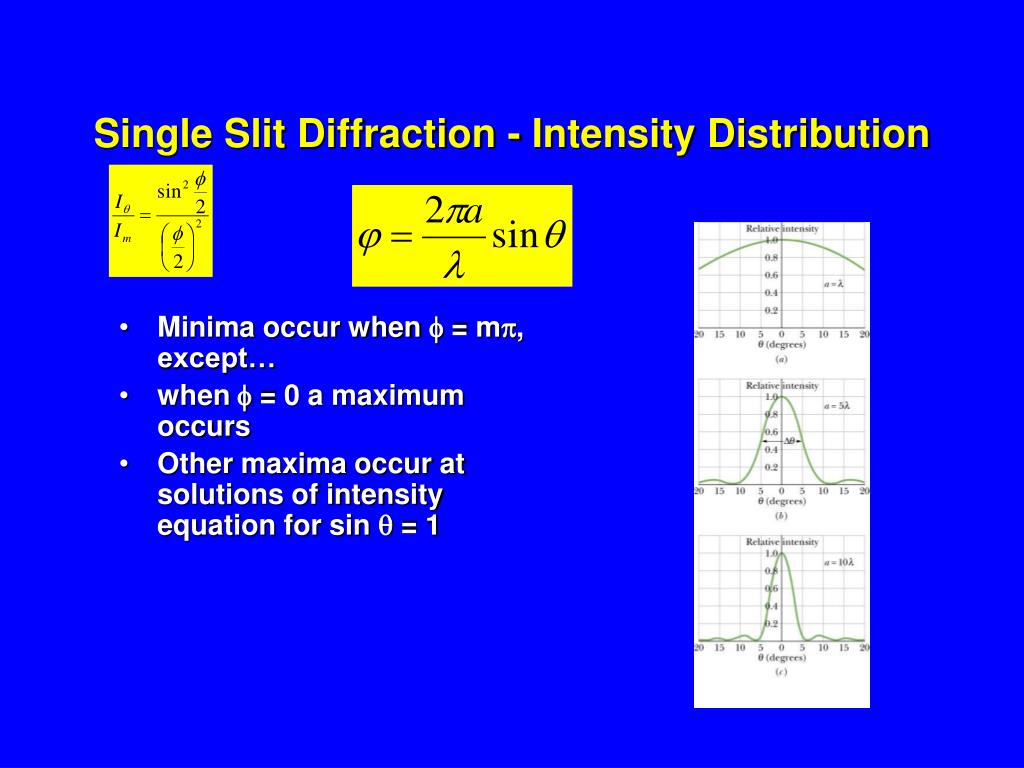
When 0 is increased enough, the head of the last phase again meets the tail of the first phasor. This arrangement corresponds to the first side maximum in the diffraction pattern. If we increase 0 a bit more, the resulting shrinkage of the coil decreases Eo, which means that the intensity also decreases. Amplitude Eo now increases until it reaches a maximum value in the arrangement shown in. Now we turn to a more general problem: find a expression for the intensity I of the pattern as a function of e, the angular position a point on a viewing screen. To do this, we divide the slit of ♴a into N zones of equal widths to small enough that we can assume each zone acts-as a source of Huygens wave We wish to superimpose the wavelets arriving at an arbitrary point P on the viewing screen, at angle e to the central axis, so that we can determine the amplitude.Īs we continue to increase 0, the angle IlcP between adjacent phasors continues to increase, the chain of phasors begins to wrap back on itself, and the resulting coil begins to shrink.

#Formula for single slit diffraction minima how to#
In Section 37-2 we saw how to find the positions of the minima and the maxima i a single-slit diffraction pattern.

Intensity in Single Slit Diffraction Qualitatively


 0 kommentar(er)
0 kommentar(er)
